基础--绘图中篇

GIF1

写在前面

本文将讲述如何在Unity中绘制数学曲面。此文旨在为渲染打下基础，可视化的观察、感受各类简单的数学曲面。全篇难度很低，放心阅读。如果想知道如何绘制数学曲线，比如心形线，欢迎阅读我的上一篇博客基础–绘图上篇。

在PC前的各位读者，建议下载MD文件阅读，观感更好。若有图片无法显示，请开启网络。欢迎转载，只需注明转载来源地址即可。MD文件及工程Package下载地址（提取码：82kk）

1.准备工作

创建一个新场景，然后在新场景中创建一个空物体，取名为”MathematicalSurfaces”，它将成为我们与Unity交互的主入口。

创建一个Cube，取名为”Point3D”，即为以后我们图像上绘制的小点；为Cube创建一个材质球”Point3DMat”和一个Shader脚本”Point3DColor”，将Shader脚本赋给材质球，然后将材质球赋给Cube。我们要通过Shader脚本为图像着色，通过颜色来反映图像上小点的空间位置信息。将Cube做成预制体，后续我们要加载此预制体。

本次将继续沿用上一篇博客中的Shader代码，以及”GraphFunction3D”脚本。创建一个新的脚本”MathematicalSurfaces”，将其拖拽到场景中的物体”MathematicalSurfaces”上。

2.绘制简单曲面

上一篇博客我们绘制的第一个曲线是Sin曲线，本篇第一个要绘制的曲面也是由Sin曲线拓展得到。

我们可以将两个维度的正弦曲线：x维度和z维度叠加成为一个曲面：

        private static Vector3 PerSine2DFunction(float x, float z, float t)
        {
            Vector3 p;
            p.x = x;
            p.y = (float)Math.Sin(PI * (x + t));
            p.y += (float)Math.Sin(PI * (z + t));
            p.y *= 0.5f;//叠加之后恢复高度
            p.z = z;
            return p;
        }

得到的图形结果：

GIF2

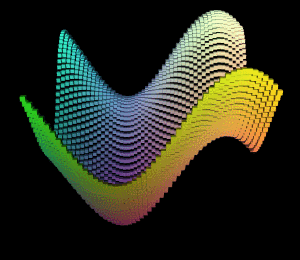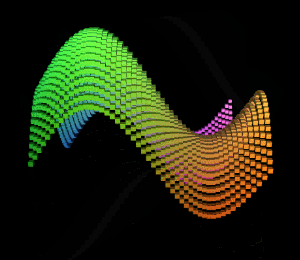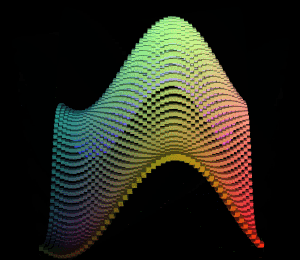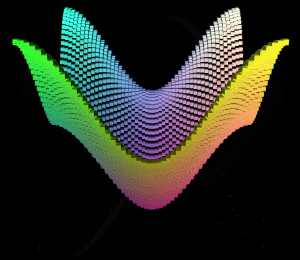
从xz平面的对角线看过去：

GIF3

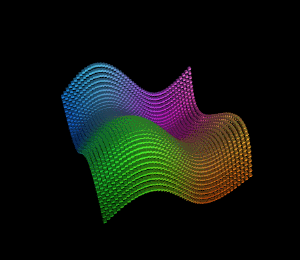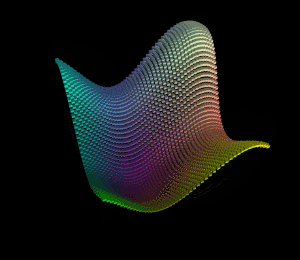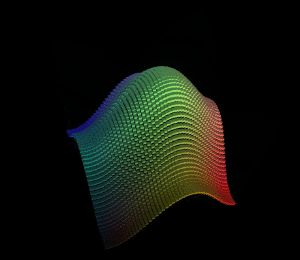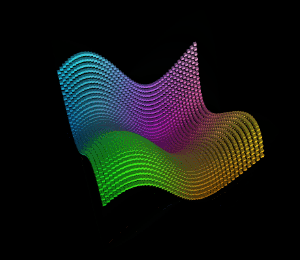
明显可以看出波浪是沿着xz平面对角线在波动。

接下来绘制另一种沿对角线波动的Sin曲面

        private static Vector3 DiagonalSine2DFunction(float x, float z, float t)
        {
            Vector3 p;
            p.x = x;
            p.y = (float)Math.Sin(PI * (x + z + t));
            p.z = z;
            return p;
        }

得到的图形结果：

GIF4

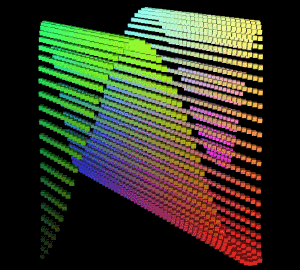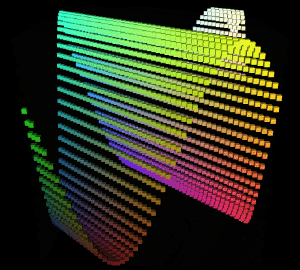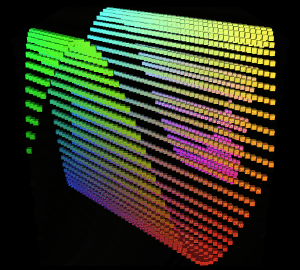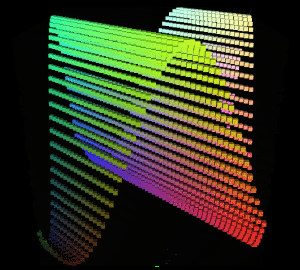
此图形没有多重波形叠加，只有一个沿着xz平面对角线的Sin波，所以绘制出来的图形虽然也是沿xz平面对角线波动，但和之前的x维度和z维度叠加成的曲面不太一样。

3.绘制多重Sin波叠加曲面

通过上一节我们知道了，不同维度的Sin波叠加可以绘制成Sin波曲面。接下来，我们叠加3个Sin波：

1.一个振幅最大的沿xz平面对角线的主波，我们为其设置4倍振幅，但动画速度降低为平常的一半：p.y = 4f * (float)Math.Sin(PI * (x + z + t * 0.5));

2.第一次波，沿x轴的Sin波，普通振幅和速度：p.y += (float)Math.Sin(PI * (x + t));

3.第二次波，沿z轴的小振幅的高频高速Sin波，一半的振幅，但是有2倍的速度和频率：p.y += 0.5f * (float)Math.Sin(2f * PI * (z + t * 2f));

        private static Vector3 MultiSine2DFunction(float x, float z, float t)
        {
            Vector3 p;
            p.x = x;
            p.y = 4f * (float)Math.Sin(PI * (x + z + t * 0.5));//主波：缓慢的对角正弦波
            p.y += (float)Math.Sin(PI * (x + t));//第一次波：沿x的正弦波
            p.y += 0.5f * (float)Math.Sin(2f * PI * (z + t * 2f));//第二次波：沿z的高频率快速移动的正弦波
            p.y *= 2f / 11f;//恢复值域
            p.z = z;
            return p;
        }

得到的图形结果：

GIF5

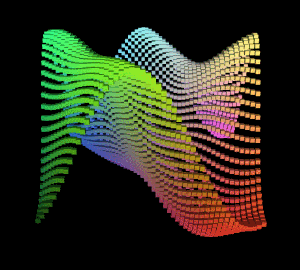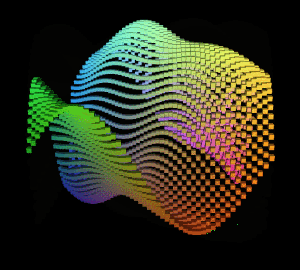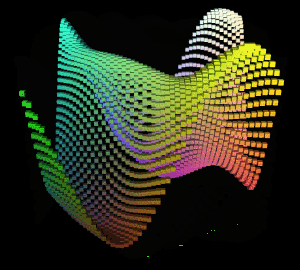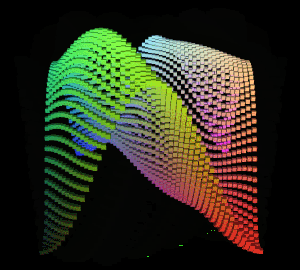
此时可以观察到缓慢的主波，由于其振幅最大，即对最终图形的y轴信息贡献最高，所以可以明显观察到。

4.绘制波纹曲面

接下来我们绘制一个比较有趣的曲面，类似于水滴滴在水面上，水面泛起的波纹。

我们知道波纹有以下特点：1.波纹中心有最大的振幅；2.波浪由中心向周围辐射散去；3.距离中心越远波浪振幅加速降低。

根据特点我们可以先定义一个曲面上任意点和中心之间的距离，此处可以使用欧式距离，比较好理解float d = (float)Math.Sqrt(x * x + z * z);

由于波浪由中心向周围辐射散去，可知波浪散去的形状应该是一个Sin波，Sin波高低周期性起伏，和波浪散开十分相似p.y = (float)Math.Sin(4f * PI * (d - 0.5f * t));[^此处为什么是减去t？]

特点3中提到距离中心越远波浪振幅加速降低，我们可以用一个反函数来描述这一加速降低过程：用1/和中心之间的距离，为了避免正中心点的高度突变，我们在分母中加上一个非零常量p.y /= 1f + 10f * d;

        private static Vector3 RippleFunction(float x, float z, float t)
        {
            Vector3 p;
            p.x = x;
            float d = (float)Math.Sqrt(x * x + z * z);
            p.y = (float)Math.Sin(4f * PI * (d - 0.5f * t));
            p.y /= 1f + 10f * d;
            p.z = z;
            return p;
        }

得到的图形结果：

GIF1

写在最后

还有许许多多有意思的曲面可以绘制，读者可以自行尝试。绘图中篇到此就结束了，感谢阅读！

下一篇：基础–绘图下篇

Reference

Mathematical Surfaces Sculpting with Numbers

基础--绘图中篇

目录

写在前面

1.准备工作

2.绘制简单曲面

3.绘制多重Sin波叠加曲面

4.绘制波纹曲面

写在最后