
目录
[TOC]
写在前面
本文将讲述如何在Unity中绘制数学曲线。此文旨在为渲染打下基础,可视化的观察、感受各类数学曲线。全篇难度很低,放心阅读。
在PC前的各位读者,建议下载MD文件阅读,观感更好。若有图片无法显示,请开启网络。欢迎转载,只需注明转载来源地址即可。MD文件及工程Package下载地址(提取码:82kk)
1.准备工作
首先调整摄像机,让我们可以刚好观察到xy平面,以后的图像都会绘制在xy平面上。
在场景中创建一个空物体,取名为”BuildingAGraph”,它将成为我们与Unity交互的主入口。
创建一个Cube,取名为”Point”,即为以后我们图像上绘制的小点;为Cube创建一个材质球”PointMat”和一个Shader脚本”PointColor”,将Shader脚本赋给材质球,然后将材质球赋给Cube。我们要通过Shader脚本为图像着色,通过颜色来反映图像上小点的空间位置信息。将Cube做成预制体,后续我们要加载此预制体。
2.绘制简单曲线
首先,我们需要明确曲线绘制的范围,为了便于我们观察,我们规定曲线绘制在[-1,1]之间,即曲线上的点在xyz坐标轴上的取值范围均为[-1,1]。
好了,在规定好绘图区域后,我们可以开始了。
我们选择使用Cube作为图上的小点,为了方便实例化Cube,我们定义一个公共变量,以便在编辑器下通过拖拽轻松获取Cube的引用[^可以做得更好吗?]。
public Transform PointPrefab;
我们需要在[-1,1]范围内生成多少个Cube以满足我们绘图的目的呢?我们可以把这个变化点抽象出来,做成公共变量便于我们修改调整。我们为其取名为分辨率Resolution,即绘制一个面上的曲线一共需要多少个Cube(像素点)。
[Range(10, 100)]
public int Resolution = 10;// 分辨率
在绘图时会创建许多Cube,为此我们使用一个数组来存储。
private Transform[] mPoints;
下面要开始写比较重要的函数了:我们的绘图函数。我们需要在函数中创建出所有我们需要的Cube,将其存放在我们定义的数组中,以便后续绘图使用。数组大小如何规定呢?由于分辨率Resolution定义的是一个面上(xy平面)Cube的个数,在后续绘图中我们还需要处理z轴方向的事情,也就是我们会扩展到绘制3D曲面,所以此处我们超前一点将数组的大小定义为分辨率的平方[^平方的含义]。
private void BuildGraph()
{
mPoints = new Transform[Resolution * Resolution];//Resolution个切片组成
}
我们知道一个原始的Cube默认大小Scale为(1,1,1),而我们规定了绘图范围[-1,1]以及分辨率,所以我们需要处理每个Cube的大小,让其适应我们的分辨率大小。
private void BuildGraph()
{
......
float step = 2f / Resolution;
Vector3 scale = Vector3.one * step;
}
现在我们可以加载我们的点Cube了,加载之后,设置它的Scale、父节点,并将其添加到数组中。
private void BuildGraph()
{
......
for (int i = 0; i < mPoints.Length; i++)
{
Transform point = Instantiate(PointPrefab);
point.localScale = scale;
point.SetParent(transform, false);
mPoints[i] = point;
}
}
在Unity的生命周期函数的Start中对所有Cube进行加载。
private void Start()
{
BuildGraph();
}
在加载完成之后,我们需要在Update中每帧更新我们的Cube位置,来显示我们的图形。我们将图像更新的方法提取成一个单独的方法[^为什么需要图像更新方法]。
现在我们有两个思路,一个是通过动画显示绘图的过程,一个是直接在一帧中绘制完成。我们可以先简单点,将动画部分放到后面完成。
我们可以先固定一个z值,然后绘制xy平面的图形,然后在沿着z轴,依次绘制在不同z值下的xy平面。那么问题来了,如果在三维空间下绘制图形的话,我们每个图形上的点都需要三个信息,即三个坐标轴上的坐标。我们如何确定每个Cube的三维坐标呢?方法很简单,就像我们在中学学到的一样:我们首先确定两个坐标,比如x轴上的和z轴上的,然后根据我们想绘制的曲线的方程来求出y轴坐标。
这里说到了曲线方程,我们知道曲线方程有显式和隐式之分[^什么叫做显式隐式?]。对于隐式的处理比较复杂,我们先来看看简单的显式方程。对于每一个方程我们应该将他们单独提取成一个函数,即输入参数x和z的值,返回y值。比如我们先来看看最简单的正弦函数。[^x为什么要乘以π?]
在往后的图形绘制中,我们会经常用到π这个常量,所以我们索性直接将其定义为const常量,方便后续使用。
private const float PI = (float)Math.PI;
正弦函数:
private static Vector3 SineFunction(float x, float z)
{
Vector3 p;
p.x = x;
p.y = (float)Math.Sin(PI * x);
p.z = z;
return p;
}
然后将曲线方程应用到图形更新函数中。应用的方法有很多种:可以直接在方法内部使用,也可以作为参数传递给方法。为了后续的扩展方便,我们选择使用委托,将曲线方法当做参数传递给图形更新函数。我们新建一个脚本”GraphFunction3D”来存放我们定义的委托。
public delegate Vector3 GraphFunction3D(float x, float z);
如此一来我们可以将曲线方法当做参数传递给图形更新函数了。
private void UpdateGraph(GraphFunction3D function)
{
float step = 2f / Resolution;
float z = 1f;
float v = -1f + step * z;
for (int x = 0, i = 0; x < Resolution; x++, i++)
{
float u = -1f + step * x;
mPoints[i].localPosition = function(u, v, t * AnimSpeed);
}
}
我们在Update中调用图形更新函数
private void Update()
{
UpdateGraph(SineFunction);
}
现在让我们看一看Unity绘制出来的sin曲线如何吧,在编辑界面的检视面板中,我们拖拽好Cube预制体,并设置好Resolution为10。

第一个曲线绘制出来了,虽然很单调,但总算完成了第一步。接下来我们来丰富一下图形的颜色。
3.为图形添加颜色
打开我们之前创建好的Shader脚本,删去所有注释和不需要的主纹理贴图和颜色基调,在输入结构体中传入物体的世界空间下的坐标,在表面函数中通过物体世界空间坐标为反照率[^反照率Albdo]赋值
Shader "Custom/PointColor"
{
Properties
{
_Glossiness ("Smoothness", Range(0,1)) = 0.5
_Metallic ("Metallic", Range(0,1)) = 0.0
}
SubShader
{
Tags { "RenderType"="Opaque" }
LOD 200
CGPROGRAM
#pragma surface surf Standard fullforwardshadows
#pragma target 3.0
struct Input
{
float3 worldPos;
};
half _Glossiness;
half _Metallic;
UNITY_INSTANCING_BUFFER_START(Props)
UNITY_INSTANCING_BUFFER_END(Props)
void surf (Input IN, inout SurfaceOutputStandard o)
{
o.Albedo.rgb = IN.worldPos.xyz * 0.5+0.5;
o.Metallic = _Metallic;
o.Smoothness = _Glossiness;
o.Alpha = 1;
}
ENDCG
}
FallBack "Diffuse"
}
由于我们规定各坐标轴上的点的坐标的取值范围为[-1,1],所以通过此操作o.Albedo.rgb = IN.worldPos.xyz * 0.5+0.5;可以将值域映射到[0,1],以满足颜色显示的需求。直接将透明度设置为1o.Alpha = 1;,我们不需要物体透明。
现在,让我们来看一看拥有颜色的图形是什么样的吧。
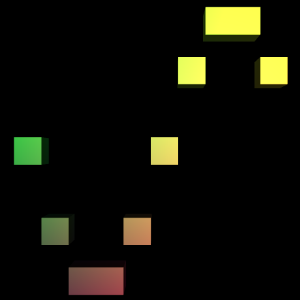
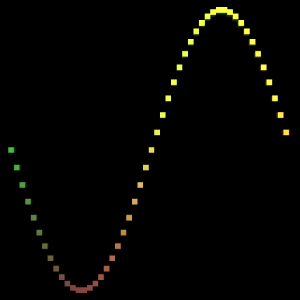
看起来好多了,现在图形上点的x坐标反映了R颜色通道,y坐标反映了G颜色通道,z坐标反映了B颜色通道。但现在图形显示得太不流畅了,我们来提高一点分辨率,将Resolution值由10提高到50,来看看效果如何。
4.让图形动起来
现在我们已经绘制出来了一条拥有颜色信息的曲线,接下来我们来稍作修改,为图形丰富一点运动元素。如何让静态的图形运动呢?答案很简单,就是为曲线方程添加一个可以随时间变化的变量,那么,当时间改变的时候,曲线方程也会变化,表现出来的就是图形动画。
给曲线方程添加时间参数 添加一个全局变量,供我们修改动画速度
[Range(0.1f, 10f)]
public float AnimSpeed = 1f;//图形动画速度
对原代码进行修改,使其支持新增参数。
先修改委托
public delegate Vector3 GraphFunction3D(float u, float v, float t);
再修改三角曲线方程
private static Vector3 SineFunction(float x, float z, float t)
{
Vector3 p;
p.x = x;
p.y = (float)Math.Sin(PI * (x + t));
p.z = z;
return p;
}
然后修改图形更新函数
private void UpdateGraph(GraphFunction3D function)
{
float t = Time.time;//游戏运行时间
float step = 2f / Resolution;
float z = 1f;
float v = -1f + step * z;
for (int x = 0, i = 0; x < Resolution; x++, i++)
{
float u = -1f + step * x;
mPoints[i].localPosition = function(u, v, t * AnimSpeed);
}
}
现在回到Unity中看看运动的Sin曲线。
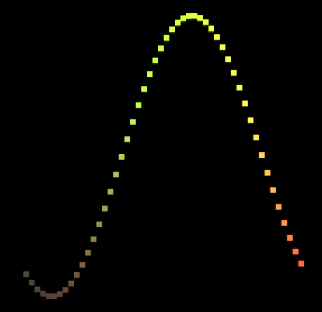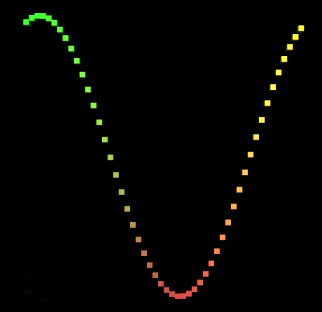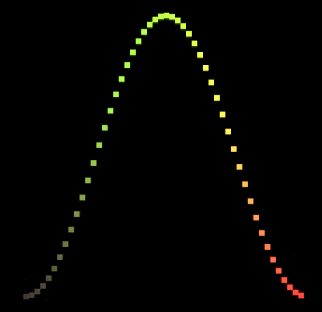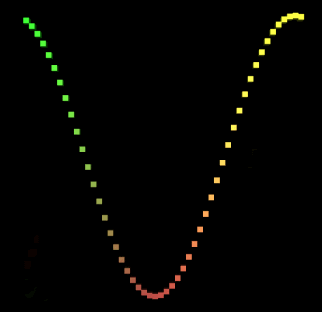
5.支持更多图形绘制
完成了第一个图形绘制后,我们在开始第二个吧,不过在开始之前我们得做一点小小的改进。我希望能在编辑模式下方便的切换我们要绘制的图形。如何做呢?不难,我们需要一个枚举,因为Unity会为我们的枚举在检视面板序列化为下拉菜单,这将非常有助于我们选择图形。我们将枚举放入脚本”GraphFunction3D”中。
public enum GraphFunction3DName
{
/// <summary>
/// 正弦函数
/// </summary>
Sine,
//TOADD
}
然后在脚本”BuildingAGraph”中加上公共变量
public GraphFunction3DName GraphFunction3DName; //图形函数(枚举)
之后检视面板会如下显示:
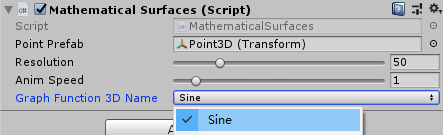
还没有结束,我们更改了编辑器下的图形函数后并不能直接作用在代码上,因为我们还没有建立枚举和图形函数之间的关联。我们知道枚举的本质其实是int类型整数,所以我们可以构建一个图形函数的数组,将所有的图形函数放入数组中,然后根据枚举来从数组中获取对应的图形函数。
private static GraphFunction3D[] mGraphFunction3Ds =
{
SineFunction,
};
我们修改Update函数
private void Update()
{
UpdateGraph(mGraphFunction3Ds[(int)GraphFunction3DName]);
}
好了,现在我们已经可以支持后续图形方法的添加了,无论是添加方法还是切换图形函数都很方便。
6.更多的图形
前面的Sin函数实在是过于简单了,现在,我们来将其复杂化一点。我们将两个Sin曲线叠加。
private static Vector3 MultiSineFunction(float x, float z, float t)
{
Vector3 p;
p.x = x;
p.y = (float)Math.Sin(PI * (x + t));//原始正弦
p.y += (float)Math.Sin(2f * PI * (x + t)) * 0.5f;//叠加等比例缩小一半的正弦
p.y *= 2f / 3f;//恢复值域
p.z = z;
return p;
}
之后修改枚举和图形函数数组,之后若再添加图形也是同此处一样,所以不再赘述。
public enum GraphFunction3DName
{
/// <summary>
/// 正弦函数
/// </summary>
Sine,
/// <summary>
/// 多重正弦函数
/// </summary>
MultiSine,
//TOADD
}
private static GraphFunction3D[] mGraphFunction3Ds =
{
SineFunction,
MultiSineFunction,
};
得到的图形结果:
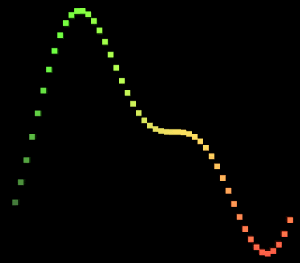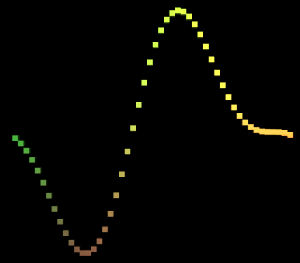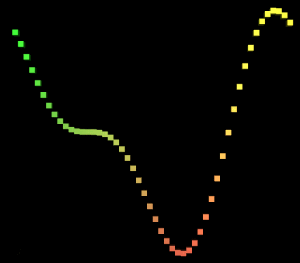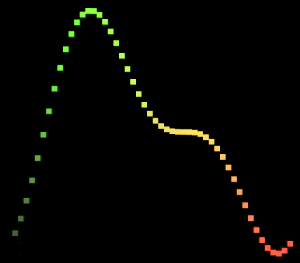
我们可以很清晰的看到一大一小两个Sin曲线的叠加。
7.绘制心形线
下面我们来绘制点有意思的曲线吧,之前绘制的都是显式曲线,现在我们来绘制一个隐式曲线–心形线。心形线是一个非常有名的曲线,由笛卡尔发现。
极坐标方程: 为了绘制方便,我们使用参数方程:
其中a决定了心形线的大小,a越大心形线越大。我们为a设定一个确定值,比如说0.5f。由于x的取值范围为[-1,1],而参数k的取值范围为[-π,π],所以我们可以将x乘以π,使其符合k的定义域以代替k。
private static Vector3 CardioidFunction(float k, float a, float t)
{
Vector3 p;
a = 0.5f;
k *= PI;
p.y = a * (2f * Mathf.Cos(k) - Mathf.Cos(2f * k));
p.x = a * (2f * Mathf.Sin(k) - Mathf.Sin(2f * k));
p.z = 0;
return p;
}
此处我们暂时去掉了图形的动画效果,得到的图形结果:

我们可以为图形绘制添加绘制动画,这样一来我们可以清楚看见图形的绘制过程。
此处我们使用Unity中的协程函数,添加一个Graph的绘图方法。
private IEnumerator Graph(GraphFunction3D function)
{
float t = Time.time;//游戏运行时间
float step = 2f / Resolution;
float z = 1f;
float v = -1f + step * z;
for (int x = 0, i = 0; x < Resolution; x++, i++)
{
yield return new WaitForSeconds(0.03f);
float u = -1f + step * x;
mPoints[i].localPosition = function(u, v, t * AnimSpeed);
}
}
每隔0.03秒绘制一个Cube,直到所有Cube绘制完成。接下来我们修改图形更新函数,在其中开启协程函数。
private void UpdateGraph(GraphFunction3D function)
{
//float t = Time.time;//游戏运行时间
//float step = 2f / Resolution;
//float z = 1f;
//float v = -1f + step * z;
//for (int x = 0, i = 0; x < Resolution; x++, i++)
//{
// float u = -1f + step * x;
// mPoints[i].localPosition = function(u, v, t * AnimSpeed);
//}
StartCoroutine(Graph(function));
}
得到的图形结果:

现在已经很好的绘制心形线了,但是图形看起来有点太”规矩”了,太规整了就不太自然,缺乏生机。我们将在下一节中加入点随机性使其看起来更自然、更有生机。
8.加入随机性
加入随机性并不困难,我们只需要在绘图函数中稍作修改:
1.图形的分辨率太低了,我们可以调整分辨率,提升Resolution到200,这样一来,图形会拥有更多点、更多细节信息。
2.提升分辨率之后,Cube会变得很小,心形线边缘会变得非常细,不太美观。我们可以增加Cube的Scale来解决此问题,将Scale随机提升5~16倍。
3.然后赋予Cube随机旋转,设置其最大旋转度数为45°,Cube会随机旋转[-45°,45°]。
修改绘图函数:
private void BuildGraph(GraphFunction3D function)
{
mPoints = new Transform[Resolution * Resolution];//Resolution个切片组成
float step = 2f / Resolution;
float maxRotate = 45f;//最大随机旋转度数
for (int i = 0; i < mPoints.Length; i++)
{
Vector3 scale = Vector3.one * step;
scale.x *= UnityEngine.Random.Range(5, 16);//随机增加Cube大小
Transform point = Instantiate(PointPrefab);
point.localScale = scale;
point.localRotation = Quaternion.Euler(0f, 0f, UnityEngine.Random.Range(-maxRotate, maxRotate));
point.SetParent(transform, false);
mPoints[i] = point;
}
}
得到的图形结果:

写在最后
还有许许多多有意思的曲线可以绘制,读者可以自行尝试。绘制过程中可以多多加入随机性,对图形视觉体验有很大改进。绘图上篇到此就结束了,感谢阅读!
Reference
Building a Graph Visualizing Math