目录
[TOC]

一、写在前面
本文首先实现了一个简易的 AStar 寻路算法,然后在其基础上进行优化,最终性能提升约 3.371 倍。
优化内容:
- 开启列表 转为 二叉堆:显著减少搜索最小 F 值节点的时间。
- 使用两个标志位:
InOpenList和InCloseList来代替Contains()/IndexOf()操作;其中IndexOf()尤其消耗性能。(标志位需要在寻路结束后重置) - 在节点中新增两个列表,用于存储:预计算的节点的邻居节点、邻居节点相对于当前节点的 G 值。可以显著提升性能。
二、基础 AStar
1.算法逻辑
算法流程如下图所示:
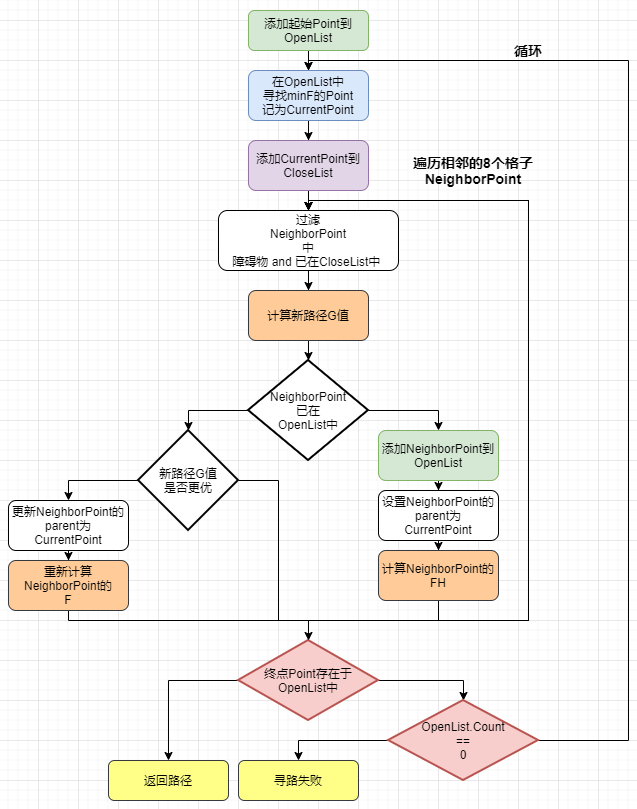
2.运行效果
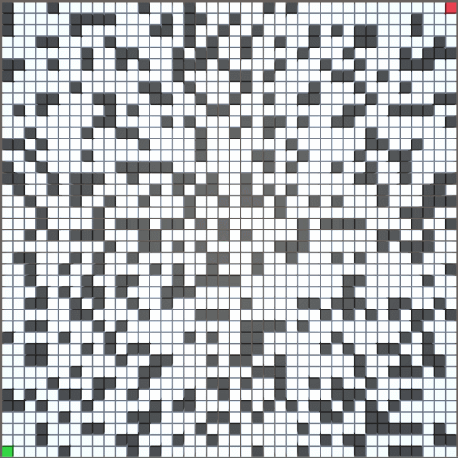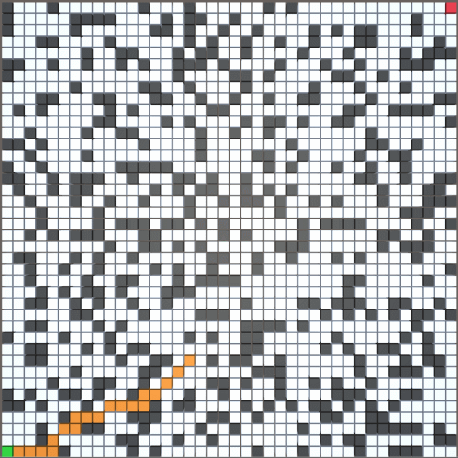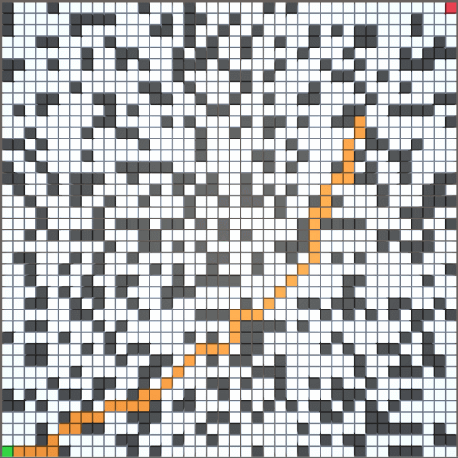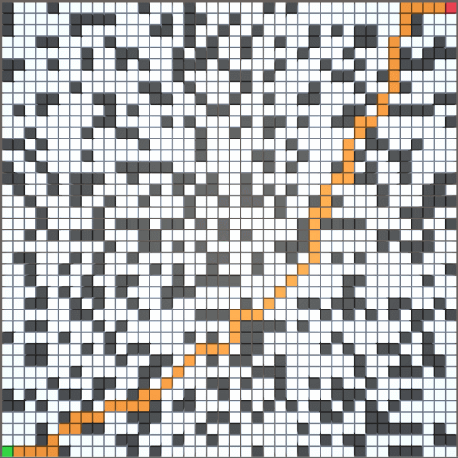
3.代码
namespace SimpleAStar
{
public class Point
{
/// <summary>
/// 父Point
/// </summary>
public Point Parent { get; set; }
public float F { get; set; }
public float G { get; set; }
public float H { get; set; }
public int X { get; set; }
public int Y { get; set; }
/// <summary>
/// 是否为障碍物
/// </summary>
public bool IsObstacle { get; set; }
public Point(int x, int y)
{
X = x;
Y = y;
Parent = null;
IsObstacle = false;
}
public void CalculateF()
{
F = G + H;
}
}
}
using System;
using System.Collections.Generic;
using UnityEngine;
using HTUtility;
namespace SimpleAStar
{
public class AStarS
{
private int mMapWidth;
private int mMapHeight;
private Point[,] mMap;
/// <summary>
/// 寻路
/// </summary>
public List<Point> FindPath(Point start, Point end)
{
List<Point> resultList = new List<Point>();//寻路结果
List<Point> openList = new List<Point>();//开启列表
List<Point> closeList = new List<Point>();//关闭列表
Point startPoint = mMap[start.X, start.Y];
Point endPoint = mMap[end.X, end.Y];
//将开始点添加到开启列表
CalculateF(startPoint, endPoint);
openList.Add(startPoint);
//遍历搜索路径
while (openList.Count > 0)
{
//1.寻找开启列表中最小F值的Point
Point minFPoint = FindMinFOfOpenList(openList);
openList.Remove(minFPoint);
closeList.Add(minFPoint);
//2.获取最小F值周围的Point(非障碍物)
List<Point> surroundPointList = GetSurroundPoints(minFPoint);
//3.过滤掉关闭列表中已经存在的Point
PointsFilter(surroundPointList, closeList);
//4.遍历符合要求的周围的Point
foreach (Point surroundPoint in surroundPointList)
{
//计算新路线G值
float newG = CalculateG(minFPoint, surroundPoint) + minFPoint.G;
//a.在开启列表中已经存在此Point
//if (openList.Contains(surroundPoint))
if (openList.IndexOf(surroundPoint) > -1)
{
//若新路线的G值更小,则有意义
if (newG < surroundPoint.G)
{
surroundPoint.Parent = minFPoint;//变更父Point
surroundPoint.G = newG;//更新G值
CalculateF(surroundPoint, endPoint);//更新F值
}
}
//b.此Point不在开启列表中
else
{
openList.Add(surroundPoint);//添加到开启列表中
surroundPoint.Parent = minFPoint;//设置父Point
surroundPoint.G = newG;//G值
CalculateF(surroundPoint, endPoint);//F值
}
}
//5.如果终点已经在开启列表中,则结束循环
//if (openList.Contains(endPoint))
if (openList.IndexOf(endPoint) > -1)
{
resultList = GetParentList(endPoint);
break;
}
}
return resultList;
}
/// <summary>
/// 获取指定Point的所有父Point
/// </summary>
/// <returns></returns>
private List<Point> GetParentList(Point point)
{
List<Point> res = new List<Point>();
while (point != null)
{
res.Add(point);
point = point.Parent;
}
res.Reverse();
return res;
}
/// <summary>
/// PointList过滤器
/// 过滤掉关闭列表中已经存在的Point
/// </summary>
private void PointsFilter(List<Point> srcList, List<Point> closeList)
{
//移除关闭列表中已经存在的Point
foreach (Point item in closeList)
{
//if (srcList.Contains(item))
if (srcList.IndexOf(item) > -1)
{
srcList.Remove(item);
}
}
}
/// <summary>
/// 获取Point周围的Point
/// 如果移动规则变化,需要改动此函数!!!
/// 注意:最后的寻路路径结果与此函数中添加周围点的顺序有关
/// </summary>
private List<Point> GetSurroundPoints(Point point)
{
List<Point> surroundPointList = new List<Point>();
Point up = null, down = null, left = null, right = null,
leftUp = null, leftDown = null, rightUp = null, rightDown = null;
if (point.Y < mMapHeight - 1)
{
up = mMap[point.X, point.Y + 1];
}
if (point.Y > 0)
{
down = mMap[point.X, point.Y - 1];
}
if (point.X > 0)
{
left = mMap[point.X - 1, point.Y];
}
if (point.X < mMapWidth - 1)
{
right = mMap[point.X + 1, point.Y];
}
if (left != null && up != null)
{
leftUp = mMap[point.X - 1, point.Y + 1];
}
if (left != null && down != null)
{
leftDown = mMap[point.X - 1, point.Y - 1];
}
if (right != null && up != null)
{
rightUp = mMap[point.X + 1, point.Y + 1];
}
if (right != null && down != null)
{
rightDown = mMap[point.X + 1, point.Y - 1];
}
if (up != null && up.IsObstacle == false)
{
surroundPointList.Add(up);
}
if (down != null && down.IsObstacle == false)
{
surroundPointList.Add(down);
}
if (left != null && left.IsObstacle == false)
{
surroundPointList.Add(left);
}
if (right != null && right.IsObstacle == false)
{
surroundPointList.Add(right);
}
if (leftUp != null && leftUp.IsObstacle == false && left.IsObstacle == false && up.IsObstacle == false)
{
surroundPointList.Add(leftUp);
}
if (leftDown != null && leftDown.IsObstacle == false && left.IsObstacle == false && down.IsObstacle == false)
{
surroundPointList.Add(leftDown);
}
if (rightUp != null && rightUp.IsObstacle == false && right.IsObstacle == false && up.IsObstacle == false)
{
surroundPointList.Add(rightUp);
}
if (rightDown != null && rightDown.IsObstacle == false && right.IsObstacle == false && down.IsObstacle == false)
{
surroundPointList.Add(rightDown);
}
return surroundPointList;
}
/// <summary>
/// 寻找OpenList中最小F值的Point
/// 为null则不存在最小F值Point
/// </summary>
private Point FindMinFOfOpenList(List<Point> openList)
{
Point minFPoint = null;
float minF = float.MaxValue;
foreach (Point point in openList)
{
if (point.F < minF)
{
minF = point.F;
minFPoint = point;
}
}
return minFPoint;
}
/// <summary>
/// 计算从当前Point到目标Point的G值
/// </summary>
private float CalculateG(Point now, Point target)
{
if ((now.X - target.X) != 0 && (now.Y - target.Y) != 0)
{
return 1.4f;
}
return 1.0f;
}
/// <summary>
/// 计算当前Point的F值
/// </summary>
private void CalculateF(Point now, Point end)
{
//1.H值计算:
float h = Math.Abs(end.X - now.X) + Math.Abs(end.Y - now.Y);
//2.G值计算:
float g = 0;
//开始点
if (now.Parent == null)
{
g = 0;
}
//非开始点
else
{
//G = 父Point的G值 + 父Point到当前Point的G值
g = now.Parent.G + CalculateG(now.Parent, now);
}
//3.F值计算F = G + H
now.G = g;
now.H = h;
now.CalculateF();
}
}
}
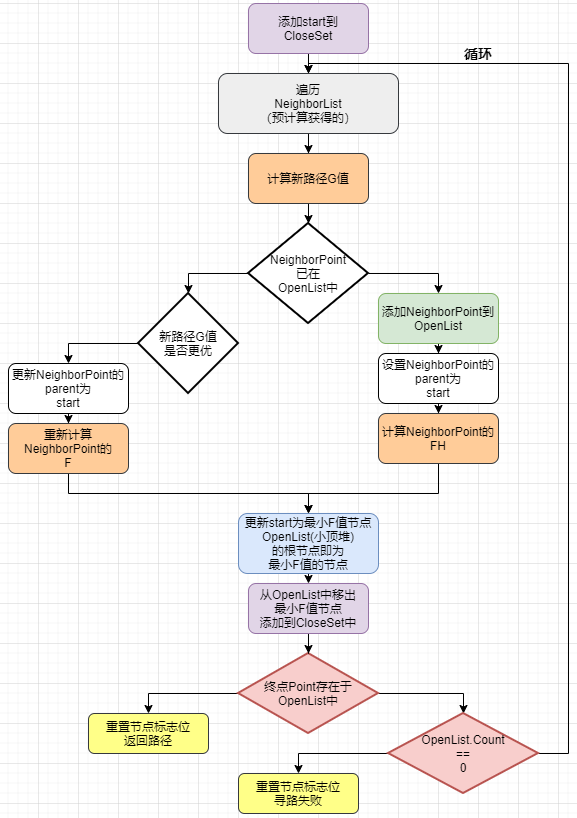
三、优化后的 AStar
1.算法逻辑
算法流程如下图所示:
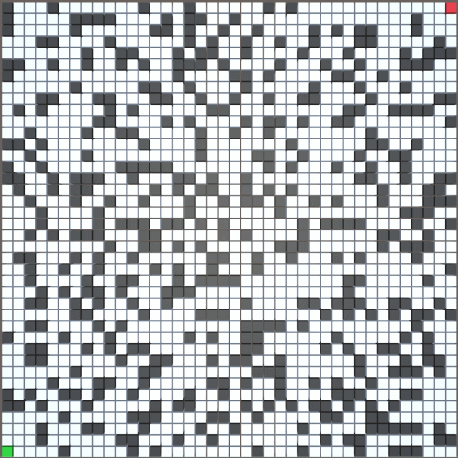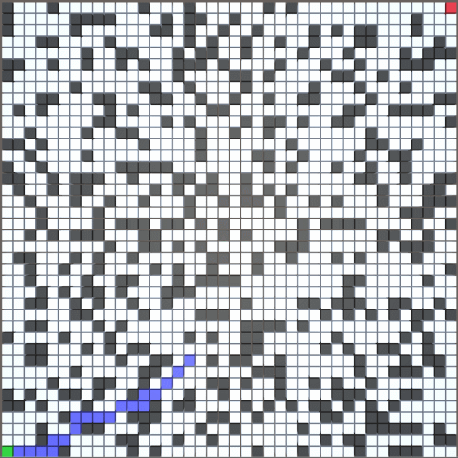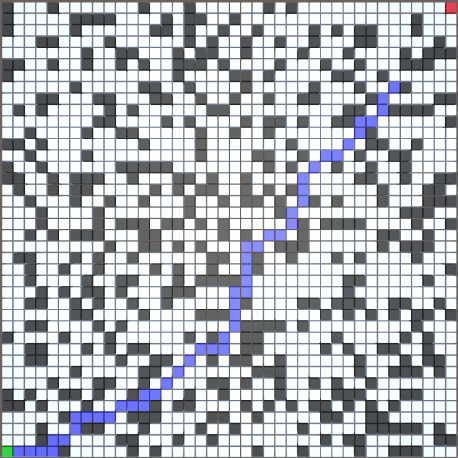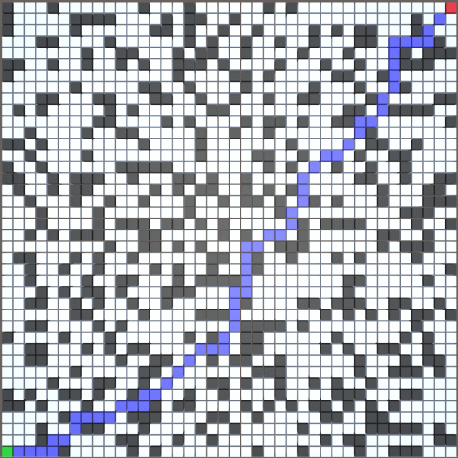
2.运行效果
3.代码
(1)节点
using System;
using System.Collections.Generic;
namespace AStar
{
[Serializable]
public enum NodeType
{
Default,
/// <summary>
/// 普通格子
/// </summary>
Normal,
}
public class Node
{
/// <summary>
/// 经过该节点的路径的总消耗
/// </summary>
public int F;
/// <summary>
/// 从起点到该节点的消耗
/// </summary>
public int G;
/// <summary>
/// 从该节点到终点的消耗
/// </summary>
public int H;
public int X;
public int Y;
/// <summary>
/// 是否是连通的(通路,非障碍物)
/// </summary>
public bool IsConnected;
public NodeType NodeType;
public Node Parent;
/// <summary>
/// 邻居节点列表
/// </summary>
public List<Node> NeighborList;
/// <summary>
/// 邻居节点的G值列表
/// </summary>
public List<int> NeighborCostG;
/// <summary>
/// 是否在 OpenList 中
/// </summary>
public bool InOpenList;
/// <summary>
/// 是否在 CloseList 中
/// </summary>
public bool InCloseList;
public Node(int x, int y, NodeType type = NodeType.Normal, bool connected = true)
{
X = x;
Y = y;
NodeType = type;
IsConnected = connected;
F = G = H = 0;
NeighborList = new List<Node>();
NeighborCostG = new List<int>();
InOpenList = InCloseList = false;
}
}
}
(2)预计算邻居节点信息
private MapMgr mMapMgr;
private List<Node> mOpenList;
private List<Node> mCloseList;
private List<Node> mRes;
private Node up, down, left, right, leftUp, leftDown, rightUp, rightDown;
/// <summary>
/// 预计算 地图中 所有节点的 相邻节点信息(地图数据发生改变的时候才需要 预计算)
/// </summary>
public void CalculateNeighborNodes()
{
for (int i = 0; i < mMapMgr.Width; i++)
{
for (int j = 0; j < mMapMgr.Height; j++)
{
CalculateNeighborNode(mMapMgr.Map[i, j]);
}
}
}
/// <summary>
/// 计算指定节点的邻居节点
/// 如果移动规则变化,需要改动此函数!!!
/// 注意:最后的寻路路径结果与此函数中添加周围点的顺序有关
/// </summary>
private void CalculateNeighborNode(Node node)
{
node.NeighborCostG.Clear();
node.NeighborList.Clear();//重新预计算的时候需要清空邻居列表(以防重复添加邻居)
up = null; down = null; left = null; right = null;
leftUp = null; leftDown = null; rightUp = null; rightDown = null;
//合法性检测
if (node.Y < mMapMgr.Height - 1)
{
up = mMapMgr.Map[node.X, node.Y + 1];
}
if (node.Y > 0)
{
down = mMapMgr.Map[node.X, node.Y - 1];
}
if (node.X > 0)
{
left = mMapMgr.Map[node.X - 1, node.Y];
}
if (node.X < mMapMgr.Width - 1)
{
right = mMapMgr.Map[node.X + 1, node.Y];
}
if (left != null && up != null)//左上不空
{
leftUp = mMapMgr.Map[node.X - 1, node.Y + 1];
}
if (left != null && down != null)//左下不空
{
leftDown = mMapMgr.Map[node.X - 1, node.Y - 1];
}
if (right != null && up != null)//右上不空
{
rightUp = mMapMgr.Map[node.X + 1, node.Y + 1];
}
if (right != null && down != null)//右下不空
{
rightDown = mMapMgr.Map[node.X + 1, node.Y - 1];
}
if (up != null && up.IsConnected == true)//上
{
node.NeighborList.Add(up);
node.NeighborCostG.Add(10);
}
if (down != null && down.IsConnected == true)//下
{
node.NeighborList.Add(down);
node.NeighborCostG.Add(10);
}
if (left != null && left.IsConnected == true)//左
{
node.NeighborList.Add(left);
node.NeighborCostG.Add(10);
}
if (right != null && right.IsConnected == true)//右
{
node.NeighborList.Add(right);
node.NeighborCostG.Add(10);
}
if (leftUp != null && leftUp.IsConnected == true
&& left.IsConnected == true && up.IsConnected == true)//左上
{
node.NeighborList.Add(leftUp);
node.NeighborCostG.Add(14);
}
if (leftDown != null && leftDown.IsConnected == true
&& left.IsConnected == true && down.IsConnected == true)//左下
{
node.NeighborList.Add(leftDown);
node.NeighborCostG.Add(14);
}
if (rightUp != null && rightUp.IsConnected == true
&& right.IsConnected == true && up.IsConnected == true)//右上
{
node.NeighborList.Add(rightUp);
node.NeighborCostG.Add(14);
}
if (rightDown != null && rightDown.IsConnected == true
&& right.IsConnected == true && down.IsConnected == true)//右下
{
node.NeighborList.Add(rightDown);
node.NeighborCostG.Add(14);
}
}
(3)二叉堆优化开启列表
/// <summary>
/// 向小顶堆中添加元素
/// </summary>
private void Add(List<Node> list, Node node)
{
list.Add(node);
node.InOpenList = true;
int index = list.Count - 1;
while (index > 0 && list[index].F < list[(index - 1) / 2].F)//子节点 < 父节点
{
Swap(list, (index - 1) / 2, index);//交换父子节点
index = (index - 1) / 2;//更新 index
}
}
/// <summary>
/// 删除小顶堆中堆顶元素,然后调整小顶堆
/// </summary>
private void RemoveFirst(List<Node> list)
{
if (list.Count == 1)
{
list[0].InOpenList = false;
list.RemoveAt(0);
//list.Clear();
return;
}
list[0].InOpenList = false;
Swap(list, 0, list.Count - 1);//交换首尾元素
list.RemoveAt(list.Count - 1);//移除尾
UpdateHeap(list, 0, list.Count);//调整堆
}
/// <summary>
/// 调整(小顶)堆,F 值最小的 Node 在堆顶
/// </summary>
/// <param 数据列表="list"></param>
/// <param 待调整的数据的索引="i"></param>
/// <param 数据列表长度="len"></param>
private void UpdateHeap(List<Node> list, int i, int len)
{
Node temp = list[i];//记录待 调整 的值
for (int k = 2 * i + 1; k < len; k = 2 * k + 1)
{
if (k + 1 < len)//存在右节点
{
if (list[k + 1].F < list[k].F)//右节点 < 左节点
{
k += 1;//选择较小的右节点
}
}
//(左/右)子节点 < 父节点
if (list[k].F < temp.F)
{
Swap(list, k, i);//交换(要保证父节点一定小于子节点——小顶堆)
i = k;//更新 i ,继续下一次循环
}
//子节点>父节点
else
{
break;//跳出循环,此处不需要往深层次遍历的原因在于:在堆排序中是从最后一个非叶子节点开始倒着向前 UpdateHeap
}
}
}
private void Swap(List<Node> list, int a, int b)
{
Node temp = list[a];
list[a] = list[b];
list[b] = temp;
}
(4)主逻辑
/// <summary>
/// AStar寻路
/// </summary>
/// <param 起点="startPos"></param>
/// <param 终点="endPos"></param>
/// <returns></returns>
public List<Node> FindPath(Vector2 startPos, Vector2 endPos)
{
//1.传入点的合法性检验:
//边界检验
if (startPos.x < 0 || startPos.x >= mMapMgr.Width
|| startPos.y < 0 || startPos.y >= mMapMgr.Height
|| endPos.x < 0 || endPos.x >= mMapMgr.Width
|| endPos.y < 0 || endPos.y >= mMapMgr.Height) return null;
//从 Map 中获取 PointNode
Node start = mMapMgr.Map[(int)startPos.x, (int)startPos.y];
Node end = mMapMgr.Map[(int)endPos.x, (int)endPos.y];
//不可为障碍物
if (start.IsConnected == false || end.IsConnected == false) return null;
//2.初始化寻路
mOpenList.Clear();
mCloseList.Clear();
mRes.Clear();
//3.将开始点放入关闭列表
start.Parent = null;
start.G = 0;
start.H = 0;
start.F = start.G + start.H;
start.InCloseList = true;
mCloseList.Add(start);
while (true)
{
//4.寻找周围的点 并放入开启列表中
FindNearlyNodeToOpenList(start, end);
//周围无通路
if (mOpenList.Count == 0)
{
//HTLogger.Warning("AStar寻路失败,周围无通路!");
//重置 标志位
for (int i = 0; i < mCloseList.Count; i++)
{
mCloseList[i].InCloseList = false;
}
for (int i = 0; i < mOpenList.Count; i++)
{
mOpenList[i].InOpenList = false;
}
return null;
}
//5.从开启列表中找到 F 最小的(小顶堆的根节点)
//6.放入关闭列表
mCloseList.Add(mOpenList[0]);
mOpenList[0].InCloseList = true;
//7.更新StartPoint
start = mOpenList[0];
//8.移出开启列表
RemoveFirst(mOpenList);
//9.退出循环条件:找到终点
if (start == end) break;
}
//重置 标志位
for (int i = 0; i < mCloseList.Count; i++)
{
mCloseList[i].InCloseList = false;
}
for (int i = 0; i < mOpenList.Count; i++)
{
mOpenList[i].InOpenList = false;
}
return GetPathRes(end);
}
/// <summary>
/// 寻找当前节点周围的合法节点,并将其加入到 OpenList 中
/// </summary>
/// <param 当前节点="parent"></param>
/// <param 目的地="end"></param>
private void FindNearlyNodeToOpenList(Node node, Node end)
{
//遍历周围的点
Node neighbor;
int newG;
for (int i = 0; i < node.NeighborList.Count; i++)
{
neighbor = node.NeighborList[i];
if (neighbor.InCloseList) continue;
//计算 新G
newG = node.G + node.NeighborCostG[i];
if (neighbor.InOpenList)//开启列表中已经包含此 point
{
if (newG < neighbor.G)//新G 值更小:新路线消耗更小
{
neighbor.Parent = node;//更新 parent
neighbor.G = newG;
neighbor.F = neighbor.G + neighbor.H;
}
}
else
{
//添加到开启列表
neighbor.Parent = node;
neighbor.G = newG;
neighbor.H = Math.Abs(end.X - neighbor.X) + Math.Abs(end.Y - neighbor.Y);
neighbor.F = neighbor.G + neighbor.H;
Add(mOpenList, neighbor);
}
}
}
四、测试
1.简单搭建测试环境
在 Unity 中搭建,随机生成地图,并记录寻路时间。
2.测试结果
选取20个随机地图进行测试,最后对结果取平均。
(随机地图的形态对寻路结果的影响很大,所以取多个地图的结果均值)
单个地图测试步骤:
每组寻路10次,测试20组,去掉极大极小值,然后取平均
(单次寻路的消耗)
| 算法\地图大小 | 20 * 20 | 40 * 40 | 70 * 70 | 100 * 100 | 120 * 120 |
|---|---|---|---|---|---|
| 未优化的 AStar | 0.3584ms | 3.0236ms | 7.7107ms | 10.4712ms | 23.3016ms |
| 优化后的 AStar | 0.0759ms | 0.6542ms | 2.5174ms | 5.7201ms | 8.8963ms |
| 提升倍数 | 4.722 | 4.622 | 3.063 | 1.831 | 2.619 |
优化后整体性能平均提升约 3.371 倍。
3.运行效果
以 70*70 尺寸的随机地图为例(障碍生成概率为 30%)
橙色为未优化的 AStar 寻路结果
蓝色为优化后的 AStar 寻路结果
(路线不同的原因:从 OpenList 中取最小 F 值的方法不同)

120 * 120 :

Reference